Question

Erin's playlist includes rock songs and

lyric songs. There are 18% more rock
songs than lyric songs. What is the
probability that a randomly chosen song to
listen to will be lyric?

Answer 1

0.459 or 45.9%

Explanation:

Let R be the number of rock songs on Erin's playlist.

Let L be the number of lyric songs on Erin's playlist.

Given that there are 18% more rock songs than lyric songs, this can be expressed as:

`R = L + 0.18L`

`R = 1.18L`

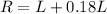
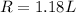
Now, the total number of songs in Erin's playlist is the sum of the lyric songs and the rock songs:

`\text{Total songs} = L + R`

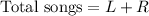
Substitute R = 1.18L into the equation to find the total number of songs in terms of lyric songs (L):

`\begin{aligned}\text{Total songs} &= L + R \\&= L + 1.18L \\&= 2.18L\end{aligned}`

The probability of randomly choosing a lyric song is given by the ratio of the number of lyric songs to the total number of songs:

`P(\text{Lyric}) = (L)/(2.18L)`

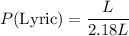
Simplify the fraction:

`P(\text{Lyric}) = (1)/(2.18)`

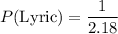
Now, calculate the probability:

`P(\text{Lyric}) =0.45871559633...`

`P(\text{Lyric}) =0.459\;\rm (3\;s.f.)`

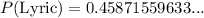
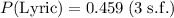
Therfeore, the probability that a randomly chosen song will be a lyric song is approximately 0.459, or 45.9%.