Answer:
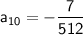
Explanation:
In a geometric progression (G.P.), the
 th term (
th term (
 ) is given by the formula:
) is given by the formula:
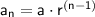
where:
-
 is the first term,
is the first term,
-
 is the common ratio, and
is the common ratio, and
-
 is the term number.
is the term number.
Given that the first term
 and the common ratio
and the common ratio
 , and we want to find the 10th term (
, and we want to find the 10th term (
 ), we can substitute these values into the formula:
), we can substitute these values into the formula:
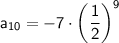
Now, calculate this value:
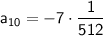
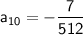
Therefore, the 10th term of the given geometric progression is
 .
.