(i)
 (ii)
(ii)
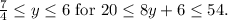
(i) Let's denote the length of the rectangular tile as L and the width as W. According to the given information:
![\[L = 4x \ \text{cm}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/3vgx0k5jsxbwuiltjll9eiyn61kqv5epwa.png)
![\[W = (x + 3) \ \text{cm}\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/elafilyju9hm8wak13qfuaagbosacdoxag.png)
The area of the rectangle is given by the formula:
![\[ \text{Area} = L * W \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/chbeamidfvgp71r4wmn5h92hxphvnsocs5.png)
We are given that the area is less than 112 cm²:
![\[4x * (x + 3) < 112\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pscvmk02mrzrpfkoomnr1e4454o664anoe.png)
Now, we can solve this inequality:
![\[4x^2 + 12x < 112\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/vuxmgdbv6zo9x615t41bypn0afdnxcxqro.png)
![\[4x^2 + 12x - 112 < 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qxdke7swkphjjs62en27tyoaw16fx6y0wg.png)
Now, factorizing the quadratic expression:
![\[(2x - 8)(2x + 14) < 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/asz6m49760vm14yfuoo3klgbu3yrm9qrcl.png)
This inequality holds true when
 and
and
 . Solving these inequalities separately, we get
. Solving these inequalities separately, we get
 However, since the length and width of the tile cannot be negative, we discard
However, since the length and width of the tile cannot be negative, we discard
 and conclude that the set of possible values for
and conclude that the set of possible values for
 is
is
 .
.
(ii) The perimeter of the second rectangular tile is given by the sum of the lengths of its four sides:
![\[P = 2(4y) + 2(y + 3) - 2y\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xtr2xz0geu19010ar2jchg9bm04dw6jwo1.png)
Simplifying this expression, we get:
![\[P = 8y + 2y + 6 - 2y = 8y + 6\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7hzgyeye04lassxzr5qo3rwddsulqx0thg.png)
We are given that the perimeter is between 20 cm and 54 cm:
![\[20 \leq 8y + 6 \leq 54\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/m28mz0azqeelyqgc0bjmoudhwofmozxllx.png)
Solving for
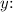
![\[14 \leq 8y \leq 48\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/qi7oqt0f9hj1oh0s2oweftumhk0bbtao5w.png)
![\[ (7)/(4) \leq y \leq 6\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/pqqg1szwo4f6z7slzb0lriggbhqt3talge.png)