The simplified expression is
 for
for
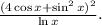
To simplify the expression
 , we'll break it down step by step. First, expand the numerator:
, we'll break it down step by step. First, expand the numerator:
![\[(4\cos x + \sin^2 x)^2 = 16\cos^2 x + 8\sin^2 x + \sin^4 x.\]](https://img.qammunity.org/2024/formulas/mathematics/college/qkn8rtyanjnqo4yvm2ybkrr4mqws9hki1n.png)
Now, substitute this back into the original expression:
![\[(16\cos^2 x + 8\sin^2 x + \sin^4 x)/(\ln x).\]](https://img.qammunity.org/2024/formulas/mathematics/college/vltlarxdk1p9a1gokqtwjm40soo1oa64ec.png)
To further simplify, factor out a common term of
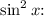
![\[(8\sin^2 x(2 + \sin^2 x) + \sin^4 x)/(\ln x).\]](https://img.qammunity.org/2024/formulas/mathematics/college/dex74dgkyd4rh2mgnjplvl3bzouvjszc36.png)
Now, factor
 from the first term in the numerator:
from the first term in the numerator:
![\[(\sin^2 x(8(2 + \sin^2 x) + \sin^2 x))/(\ln x).\]](https://img.qammunity.org/2024/formulas/mathematics/college/rczd0mvq292t73fgc56aqi8p1c43dsohst.png)
Distribute
 in the brackets:
in the brackets:
![\[(8\sin^2 x + 16\sin^2 x + \sin^4 x)/(\ln x).\]](https://img.qammunity.org/2024/formulas/mathematics/college/lpdavjbvsjvqndllsjsn346oecf9ivxjoo.png)
Combine like terms:
![\[(24\sin^2 x + \sin^4 x)/(\ln x).\]](https://img.qammunity.org/2024/formulas/mathematics/college/58a8ah2jhdd8tfu8flc1emk7jybi0ulrde.png)
This expression represents the simplified form of
 in terms of trigonometric functions and the natural logarithm.
in terms of trigonometric functions and the natural logarithm.