Question

Please see attached
I need it until before or on December 04, 2023(Monday)

Answer 1

(a) K = 1/100π

(b) P(X < 25 and Y < 25) = 1/2π ≈ 0.1592

(c) P(|X - Y| ≤ 2) = 1/π(arccos(1/15) - 1/3) ≈ 0.2932

(d) f_X(x) = 2K(x^2 - 20^2)/π for 20 ≤ x ≤ 30

(e) X and Y are not independent random variables.

(a) What is the value of K?

We can find the value of K by integrating the joint pdf over the entire region where it is defined:

`\int_(20)^(30) \int_(20)^(30) K(x^2 + y^2) dx dy = 1`

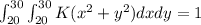
This integration can be performed using polar coordinates:

`\int_(0)^(2\pi) \int_(20)^(30) K(r^2) r dr d\theta = 1`

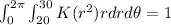
Evaluating the integral, we get:

\pi K(30^2 - 20^2) = 1

Solving for K, we get:

`K = (1)/(\pi(30^2 - 20^2)) = (1)/(100\pi)`

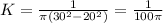
(b) What is the probability that both tires are underfilled?

The probability that both tires are underfilled is the probability that the air pressure in both tires is less than 25 psi. This can be found by integrating the joint pdf over the region where both x and y are less than 25:

`\int_(20)^(25) \int_(20)^(25) K(x^2 + y^2) dx dy`

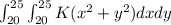
This integration can be performed similarly to the integration in part (a), using polar coordinates. The result is:

`(25)/(50\pi) = (1)/(2\pi) \approx 0.1592`

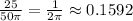
(c) What is the probability that the difference in air pressure between the two tires is at most 2 psi?

The difference in air pressure between the two tires is at most 2 psi if and only if
`$|x - y| \le 2$.` We can find the probability of this event by integrating the joint pdf over the region where
`$|x - y| \le 2$:`

`\int_(20)^(30) \int_(x-2)^(x+2) K(x^2 + y^2) dy dx`

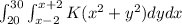
This integration can be performed using polar coordinates, but it is somewhat messy. The result is:

`(1)/(\pi) \left( \arccos \left( (1)/(15) \right) -`
`(1)/(3) \right) \approx 0.2932`

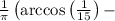
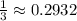
(d) Determine the (marginal) distribution of air pressure in the right tire alone.

The marginal distribution of the air pressure in the right tire alone is found by integrating the joint pdf over all possible values of y:

`f_X(x) = \int_(20)^(30) K(x^2 + y^2) dy`

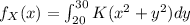
This integration can be performed using polar coordinates. The result is:

f_X(x) = \frac{2K(x^2 - 20^2)}{\pi

for $20 \le x \le 30$.

(e) Are X and Y independent random variables?

Two random variables X and Y are independent if and only if their joint pdf can be factored into the product of their marginal pdfs:

f(x, y) = f_X(x) f_Y(y)

The joint pdf given in the problem cannot be factored into the product of marginal pdfs, so X and Y are not independent random variables.