Question

Please help I can’t seem to figure this out

Answer 1

The parabola opens upward, has vertex at ,4, and has x-intercepts at 2,.

Step-by-step explanation:

(a) We can determine whether the parabola opens upward or downward by looking at the leading coefficient of the quadratic equation. The leading coefficient is the coefficient of the
`$x^2$` term. If the leading coefficient is positive, the parabola opens upward. If the leading coefficient is negative, the parabola opens downward.

(b) The x-intercepts of a parabola are the points where the parabola crosses the x-axis. The y-intercept of a parabola is the point where the parabola crosses the y-axis.

To find the x-intercepts, we set the quadratic equation equal to zero and solve for x. This gives us the following equation:

`ax^2 + bx + c = 0`

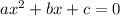
We can use the quadratic formula to solve for x:

`x = (-b \pm √(b^2 - 4ac))/(2a)`

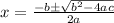
To find the y-intercept, we substitute x = 0 into the quadratic equation. This gives us the following equation:

y = f(0)

The value of
`$f(0)$` is the y-coordinate of the y-intercept. From the graph, we can see that the y-intercept is at (0, 4).

(c) The vertex of a parabola is the point where the parabola changes direction. To find the coordinates of the vertex, we can use the following formulas:

`x = (-b)/(2a)`

`y = f\left((-b)/(2a)\right)`

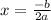
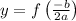
However, we can see from the graph that the vertex is at the point (0, 4).

(d)The equation of the axis of symmetry for the parabola in the image is x = 0.

This can be found by using the formula x = -b/2a, where a and b are the coefficients of the quadratic equation in standard form,
`y = ax^2 + bx + c.`

In the image, the quadratic equation is not given explicitly, but we can see that the axis of symmetry is the y-axis, which means that the x-coordinate of the vertex of the parabola is 0.

Therefore, the equation of the axis of symmetry is x = 0.

Question: