Question

the bridge is supported by triangular braces. if the sides of each braces have lengths of 55 feet, 42 feet, and 38 feet, find the measure of the angle opposite of the 42 foot side

Answer 1

The measure of the angle opposite the 42-foot side is approximately 86.71 degrees.

Using Heron's Formula for Area:

Calculate the semiperimeter (s) of the triangle: s = (a + b + c) / 2 = (55 + 42 + 38) / 2 = 67.5.

Use Heron's formula to find the area (K) of the triangle:

K =
`√((s(s - a)(s - b)(s - c)) )`

K =
`√((67.5 * (67.5 - 55) * (67.5 - 42) * (67.5 - 38)))`

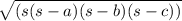
K ≈ 534.44.

The Height from Area and Base Length:

We want to find the height (h) of the triangle from the base length (b = 42 feet) and the area (K).

The formula for height from area and base is h = 2K / b. Substituting the values, we get h ≈ 25.47 feet.

Applying the Law of Cosines to Find the Angle:

We know the base length (b = 42 feet) and the two adjacent side lengths (a = 55 feet and c = 38 feet).

The Law of Cosines states: cos(C) =
`( (a^2 + b^2 - c^2))/((2ab))`

cos(C) =
`( (55^2 + 42^2 - 38^2))/((2* 55 * 42))`

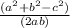
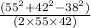
cos(C) ≈ 0.041

We want to find angle C, which is opposite the 42-foot side (base).

Plugging in the values, we get cos(C) ≈ 0.041.

Taking the inverse cosine (arccos) of both sides, we get C ≈ 86.71°.