Question

Assume that you plan to use a significance level of α = 0.05 to test the claim that p1 = p2. Use the given sample sizes and numbers of successes to find the z test statistic for the hypothesis test.

A report on the nightly news broadcast stated that 13 out of 116 households with pet dogs were burglarized and 24 out of 206 without pet dogs were burglarized.

Answer 1

The z-test statistic for the hypothesis test is approximately −0.000510

To test the claim that the proportions of households with and without pet dogs experiencing burglaries are equal, we can use the z-test for two proportions. The formula for the z-test statistic is:

`z=\frac{p_1-p_2}{\sqrt{p(1-p)((1)/(n_1) -(1)/(n_2) )} }`

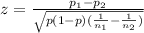
where p is the pooled sample proportion, given by:

`p= (x_1+x_2)/(n_1+n_2)`

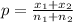
Here,
`x _1` is the number of successes in the first sample,
`n_1` is the sample size for the first group,
`x _2` is the number of successes in the second sample, and
`n_2` is the sample size for the second group.

For the given data:

`p_1 =(13)/(116)`

`p_2 = (24)/(206)`

`p=(13+24)/(116+206)`

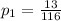
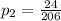
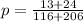
Substitute these values into the z-test formula:

`z= \frac{(13)/(116)- (24)/(206) }{\sqrt{((37)/(322)(1-(37)/(322) )((1)/(1116)+(1)/(206) ) } }`

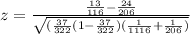
Calculate this expression to get the z-test statistic.

z ≈ −0.000510