Question

Assume the annual day care cost per child is normally distributed with a mean of ​$9000 and a standard deviation of ​$500. In a random sample of 120 ​families, how many pay more than ​$8505 annually for day care per​ child?

Answer 1

101 families

Explanation:

The annual day care cost per child is normally distributed with a mean (μ) of ​$9000 and a standard deviation (σ) of ​$500. Therefore:

`\rm X \sim N(\mu,\sigma^2)\implies \boxed{\rm X \sim N(9000,500^2)}`

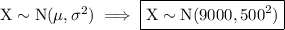
where X is the annual day care cost per child in dollars.

To calculate how many families pay more than ​$8,505 annually for day care per​ child in a random sample of 120 ​families, we first need to find P(X > 8505).

Calculator input for "normal cumulative distribution function (cdf)":

• Lower bound: x = 8505
• Upper bound: x = 15000
• σ = 500
• μ = 9000

This gives the probability that a family pays more than $8,505 annually for day care per​ child as:

`P(X > 8505)=0.8389129405`

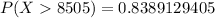
To determine how many families pay more than ​$8,505 annually for day care per​ child in a random sample of 120 ​families, multiply the found probability by 120:

`\begin{aligned}\textsf{Number of families}&=P(X > 8505)* 120\\&=0.8389129405 * 120\\&=100.66955...\\&=101\end{aligned}`

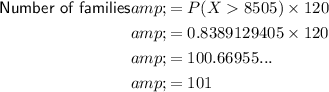
Therefore, in a random sample of 120 families, approximately 101 families are expected to pay more than $8,505 annually for day care per child.