Question

0 seconds. Its height, in

meters above sea-level, as a function of time is given by
h(t) = -4.9t² + 331t + 276.
NASA launches a rocket at t
=
Assuming that the rocket will splash down into the
ocean, at what time does splashdown occur?
The rocket splashes down after
seconds.
How high above sea-level does the rocket get at its
peak?
The rocket peaks at
level.
meters above sea-

Answer 1

The rocket splashes down after approximately 68.57 seconds.

The rocket reaches its peak at approximately 33.67 seconds.

The rocket reaches a height of approximately 13,205.93 meters above sea-level at its peak.

The equation representing the height of the rocket is

h(t)=−
`4.9t^(2)`+331t+276.

To find when splashdown occurs, set h(t) to 0:

`4.9t^(2)`+331t+276 = 0

Use Quadratic Formula
`\frac{-b +-\sqrt{b^(2) - 4ac} }{2a}`

`{b^(2) - 4ac}` =
`{b^(2) - 4ac} = {331^(2) - 4x4.9x276}` = 114,965.8

t=
`(-331 +-√(114,965.8) )/(2.-4.9)`

`t_(1) = -0.842`

`t_(2) = 68.57`

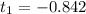
Choosing the positive root (time cannot be negative in this context) to find when splashdown occurs,
`t = 68.57`
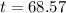
Substitute the splashdown time to h(t) to find the height at splashdown:

h(t)=−
`4.9t^(2)`+331t+276.

h(t)= 23107.17
The time at which the rocket reaches its peak is given by
`t_(peak)` =
`- (b)/(2a)` = 33.67

Substitute the peak time
`t_(peak)` back into the original equation h(t) to find the maximum height above sea-level:

`h(t_(peak) )` = 13205.93
Therefore,
The rocket splashes down after approximately 68.57 seconds.

The rocket reaches its peak at approximately 33.67 seconds.

The rocket reaches a height of approximately 13,205.93 meters above sea-level at its peak.