The projectile reaches 112 feet at 8.28 seconds in the upward motion and in 7.69 seconds in downward motion
To find the two points in time when the object is 112 feet above the ground, we can set the height equation equal to 112 and solve for t:
ℎ =
 +118t +80
+118t +80
h=112
Therefore,
 +118t +80 = 112
+118t +80 = 112
 +118t -32 = 0
+118t -32 = 0
Now, we have a quadratic equation in the form
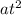 +bt+c=0, where
+bt+c=0, where
a=16,
b=118, and
c=−32.
We can solve for t using the quadratic formula:

Therefore, t=

Calculate the discriminant
 =
=
 =
=
 =126.38
=126.38
Now, substitute the values into the quadratic formula:
t=

 =
=
 = 8.28 seconds
= 8.28 seconds
 =
=
 = -7.69 seconds
= -7.69 seconds
The projectile reaches 112 feet at 8.28 seconds in the upward motion and in 7.69 seconds in downward motion