Answer:
∠V = 49°
Explanation:
In triangle VWX:
- v = 180 inches
- w = 170 inches
- ∠X = 86°
As we have the measure of two sides (v and w) and the included angle (X), we can use the cosine rule to find the length of side x, then use the sine rule to find ∠V.

So, in this case:
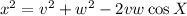
Substitute the values of v, w and X into the formula, and solve for the exact value of x:
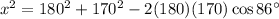
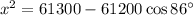
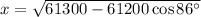
Now, we can use the sine rule to find the measure of angle V.

In this case:
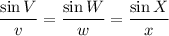
Substitute the values of v, x and X into the formula:
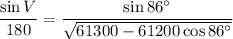
Solve for V:
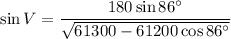
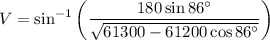
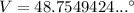
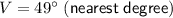
Therefore, the measure of ∠V is 49° (rounded to the nearest degree).