Question

.. An object (mass 10.0 kg) slides upward on a slippery

vertical wall. A force F of 60 N acts at an angle of 60° as
shown in Fig. 4.36.
(a) Determine the normal force
exerted on the object by the wall.
(b) Determine the
object's acceleration.

Answer 1

The object's acceleration is 3.0
`m/s^2`.

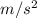To solve this problem, we can break the force F into its horizontal and vertical components. The normal force N exerted by the wall is equal to the vertical component of the force.

Given:

- Mass of the object m = 10.0 kg

- Force F = 60 N

- Angle
`(\( \theta \))` = 60°

Let's find the vertical component of the force
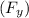`(\( F_y \))` using trigonometric functions:

`\[ F_y = F \cdot \sin(\theta) \]`

`\[ F_y = 60 \cdot \sin(60^o) \]`

`\[ F_y \approx 51.96 \, \text{N} \]`

Now, the normal force N is equal to the weight of the object plus the vertical component of the force:

`\[ N = m \cdot g + F_y \]`

where g is the acceleration due to gravity
`9.8 m/s^2`.

`\[ N = (10.0 \, \text{kg} \cdot 9.8 \, \text{m/s}^2) + 51.96 \, \text{N} \]`

`\[ N \approx 147.96 \, \text{N} \]`

So, the normal force exerted on the object by the wall is approximately 147.96 N.

To find the object's acceleration a, we can use Newton's second law:

`\[ F_{\text{net}} = m \cdot a \]`

The net force
`(\( F_{\text{net}} \))` is the horizontal component of the force:

`\[ F_{\text{net}} = F \cdot \cos(\theta) \]`

`\[ F_{\text{net}} = 60 \cdot \cos(60^o) \]`

`\[ F_{\text{net}} = 30 \, \text{N} \]`

Now, plug this into Newton's second law:

`\[ 30 = 10.0 \cdot a \]`

`\[ a = (30)/(10.0) \]`

`\[ a = 3.0 \, \text{m/s}^2 \]`

So, the object's acceleration is 3.0 m/s2.