Question

A bridge hand is made up of 13 cards from a deck of 52. Find the probability that a hand chosen at random contains at least 1 king

Answer 1

Answer: 0.6962 (approximate)

The more accurate value would be 0.6961824729892 which is also approximate.

============================================================

Step-by-step explanation

Use the nCr formula

`nCr = (n!)/(r!*(n-r)!)`

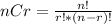
to find that 52C13 = 635,013,559,600

This number is really large. It's roughly 635 billion. It represents the number of possible 13 card hands.

Out of those roughly 635 billion hands, we need to find out how many of them have no kings at all.

There are 4 kings in the deck, so 52-4 = 48 cards that aren't a king.

Use that formula to find that 48C13 = 192,928,249,296 which is roughly 193 billion. It's the number of hands that don't have a king.

Subtract the two items

635,013,559,600 - 192,928,249,296 = 442,085,310,304

There are roughly 442 billion hands that have at least 1 king (i.e. 1 or more kings).

Divide this over the number of 13 card hands possible.

(442,085,310,304)/(635,013,559,600) = 0.6961824729892

That rounds to about 0.6962, so there's roughly a 69.62% chance of getting a hand that has at least one king. Round this however your teacher instructs.