Question

Given dy/dt=9y and y(0)=450. Find y(t)

Answer 1

Answer:
`y(t) = 450e^(9t)`

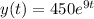
Work Shown

`(dy)/(dt) = 9y\\\\(dy)/(y) = 9 dt\\\\\displaystyle \int (dy)/(y) = \int 9 dt\\\\\ln( |y| ) = 9t+C \ \ \text{... don't forget about the plus C}\\\\|y| = e^(9t+C)\\\\|y| = e^(9t)*e^(C)\\\\|y| = e^(C)*e^(9t)\\\\|y| = Ae^(9t) \ \ \text{ .... let } A = e^C\\\\y = Ae^(9t) \ \ \text{ .... see note below}\\\\`

Note: The e^(9t) portion is always positive. Since y(0) = 450 is also positive, this means A > 0 as well. We can erase the absolute value bars.

Let's use t = 0 and y = 450 to find the value of A.

`y = Ae^(9t)\\\\450 = Ae^(9*0)\\\\450 = Ae^(0)\\\\450 = A*1\\\\450 = A\\\\A = 450`

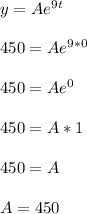
Feel free to skip a few steps if that scratch work seems a bit too wordy.

We go from
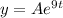`y = Ae^(9t)` to the final answer
`y = 450e^(9t)`

------------------------------------

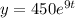
Check:

Apply the derivative with respect to t.

`y = 450e^(9t)\\\\(dy)/(dt) = (d)/(dt)\left[450e^(9t)\right]\\\\(dy)/(dt) = 9*450e^(9t) \ \ \text{ ... chain rule}\\\\(dy)/(dt) = 9y`

In the last step, I replaced the 450e^(9t) with y, which is valid because we found that y = 450e^(9t)