Question

11. A new type of band has been developed by a dental laboratory for children who have to wear braces. The new bands are designed to look better, be more comfortable, and provide more rapid progress in realigning teeth. An experiment was conducted to compare the mean wearing time necessary to correct a specific type of misalignment between the old braces and the new bands. Seventy two children were randomly assigned, 36 to each group. A summary of the data is given below.

Old Braces: n1= 36, sample mean = 420, s1 = 48 days;
New Bands: n2= 36, sample mean = 395, s2 = 50 days;

Conduct a test to see if the population mean wearing times differ using α= 0.05.

Answer 1

Independent t-test:
`\(t \approx 2.164\)`. Reject null; evidence shows significant difference in mean wearing times.

To test if the population mean wearing times for the old braces and new bands differ, we'll conduct an independent samples t-test using the provided data. Here are the steps:

1. State the Hypotheses:

Null Hypothesis (H_0): The population mean wearing times for old braces
`(\(\mu_1\))` and new bands
`(\(\mu_2\))` are equal.

`\(H_0: \mu_1 = \mu_2\)`

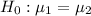
Alternative Hypothesis
`(\(H_1\))`: The population mean wearing times for old braces and new bands are not equal.

`\(H_1: \mu_1 \\eq \mu_2\)`

2. Select the Significance Level:

Given:
`\(\alpha = 0.05\)`

3. Compute the Test Statistic:

The formula for the independent samples t-test:

`\[ t = \frac{(\bar{x}_1 - \bar{x}_2) - (\mu_1 - \mu_2)}{\sqrt{(s_1^2)/(n_1) + (s_2^2)/(n_2)}}\]`

Given data:

`\(n_1 = 36, \bar{x}_1 = 420, s_1 = 48\)`

`\(n_2 = 36, \bar{x}_2 = 395, s_2 = 50\)`

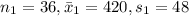
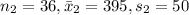
Calculating the test statistic:

`\[ t = \frac{(420 - 395) - 0}{\sqrt{(48^2)/(36) + (50^2)/(36)}}\]`

`\[ t = \frac{25}{\sqrt{(2304)/(36) + (2500)/(36)}}\]`

`\[ t = (25)/(√(64 + 69.444))\]`

`\[ t ≈ (25)/(√(133.444))\]`

`\[ t ≈ (25)/(11.55)\]`

`\[ t ≈ 2.164\]`

4. Determine the Critical Value or P-value:

Degrees of freedom
`(\(df\)) = \(n_1 + n_2 - 2 = 36 + 36 - 2 = 70\)`

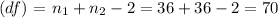
At
`\(\alpha = 0.05\) and \(df = 70\)`, the critical t-value is approximately
`\(\pm 1.997\)`(two-tailed test).

5. Make a Decision:

As
`\(|t| = 2.164 > 1.997\)` (in absolute terms), we reject the null hypothesis.

6. Conclusion:

There is sufficient evidence to conclude that the population mean wearing times for old braces and new bands are significantly different at the 0.05 significance level.