Question

Attached below is my calculus question

(A circle is inside a square. The radius of the circle is increasing at a rate of 5 meters per day..)

Thank you.

Answer 1

-340.5 m²/day

Explanation:

You want to know the rate of change of area between a 12 m circle within a 19 m square when the radius is increasing at 5 m/day and the square's side is decreasing at 4 m/day.

Area

The difference in areas is ...

∆A = s² -πr²

The rate of change is ...

∆A' = 2s·s' -2πr·r'

∆A' = 2(19 m)(-4 m/day) -2π(6 m)(+5 m/day)

= (-152-60π) m²/day ≈ -340.50 m²/day

The area is changing at about -340.5 square meters per day.

<95141404393>

Answer 2

-340.50 square meters per day

Explanation:

Connected rates of change refers to the relationship between the rates at which two or more variables are changing with respect to a common independent variable.

A derivative represents the rate of change of a function with respect to its independent variable. So, when something changes over time, the derivative is d/dt of that variable.

We are told that a circle is inside a square.

Given that the radius (r) of the circle is increasing at a rate of 5 meters per day, then:

`\frac{\text{d}r}{\text{d}t}=5\; \sf m/day`

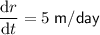
Given that the sides (s) of the square are decreasing at a rate of 4 meters per day, then:

`\frac{\text{d}s}{\text{d}t}=-4\; \sf m/day`

The area (A) outside the circle but inside the square is given by the area of the square less the area of the circle:

`A =s^2- \pi r^2`

The rate of change of this area is given by dA/dt.

To determine dA/dt, differentiate both sides of the equation with respect to time (t):

`\frac{\text{d}}{\text{d}t}\left(A\right) = \frac{\text{d}}{\text{d}t}\left(s^2\right)-\frac{\text{d}}{\text{d}t} \left(\pi r^2\right)`

`\frac{\text{d}}{\text{d}t}\left(A\right) = \frac{\text{d}}{\text{d}t}\left(s^2\right)-\pi \cdot \frac{\text{d}}{\text{d}t} \left( r^2\right)`

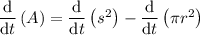
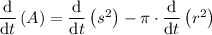
Differentiate each term using the chain rule:

`\frac{\text{d}A}{\text{d}t} =2s\cdot \frac{\text{d}s}{\text{d}t}- \pi\cdot 2r\cdot \frac{\text{d}r}{\text{d}t}`

`\frac{\text{d}A}{\text{d}t} = 2s\cdot \frac{\text{d}s}{\text{d}t}-2\pi r\cdot \frac{\text{d}r}{\text{d}t}`

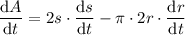
Now, substitute the given values of ds/dt = -4 and dr/dt = 5 into the equation:

`\frac{\text{d}A}{\text{d}t} = 2s\cdot (-4)-2\pi r\cdot 5`

`\frac{\text{d}A}{\text{d}t} = -8s-10\pi r`

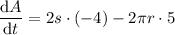
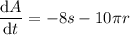
To determine how fast the area outside the circle but inside the square is changing when the radius is 6 meters and the sides are 19 meters, substitute r = 6 and s = 19 into dA/dt:

`\frac{\text{d}A}{\text{d}t} = -8(19)-10\pi (6)`

`\frac{\text{d}A}{\text{d}t} = -152-60\pi`

`\frac{\text{d}A}{\text{d}t} = -340.4955592...`

`\frac{\text{d}A}{\text{d}t} = -340.50\; \sf m^2/day\;(2\;d.p.)`

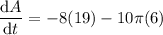
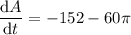
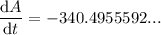
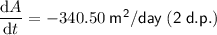
Therefore, the rate of change of the area enclosed between the circle and the square is -340.50 square meters per day.