Question

What current flows through a 2.54 cm diameter rod of pure silicon that is 28.0 cm long, when 8.00 x 103 V is applied to it? The resistivity of silicon is 2300 Ω

m.

Answer 1

The current flowing through the silicon rod is approximately
`\(0.00629 \, \text{A}\).`

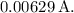
To calculate the current flowing through the silicon rod, we can use Ohm's Law, which is given by the formula:

`\[ I = (V)/(R) \]`

where:

- I is the current,

- V is the voltage applied,

- R is the resistance.

The resistance (R) of the silicon rod can be calculated using the formula for the resistance of a cylindrical conductor:

`\[ R = (\rho \cdot L)/(A) \]`

where:

-
`\( \rho \)` is the resistivity of the material (given as
`\( 2300 \, \Omega \cdot \text{m} \)` for silicon),

- L is the length of the rod,

- A is the cross-sectional area of the rod.

The cross-sectional area (A) of the rod can be calculated using the formula for the area of a circle:

`\[ A = \pi \cdot \left((d)/(2)\right)^2 \]`

where:

- d is the diameter of the rod.

Now, substitute these values into the equations to find R and then use Ohm's Law to find I.

Let's calculate it.

First, calculate the cross-sectional area (A):

`\[ A = \pi \cdot \left((d)/(2)\right)^2 \]`

`\[ A = \pi \cdot \left(\frac{2.54 \, \text{cm}}{2}\right)^2 \]`

`\[ A = \pi \cdot \left(1.27 \, \text{cm}\right)^2 \]`

`\[ A \approx \pi \cdot 1.6089 \, \text{cm}^2 \]`

`\[ A \approx 5.06 \, \text{cm}^2 \]`

Next, calculate the resistance (R):

`\[ R = (\rho \cdot L)/(A) \]`

`\[ R = \frac{2300 \, \Omega \cdot \text{m} \cdot 0.28 \, \text{m}}{0.000506 \, \text{m}^2} \]`

`\[ R \approx \frac{644 \, \Omega \cdot \text{m} \cdot \text{m}}{0.000506 \, \text{m}^2} \]`

`\[ R \approx 1272727.27 \, \Omega \]`

Now, use Ohm's Law to find the current (I):

`\[ I = (V)/(R) \]`

`\[ I = \frac{8000 \, \text{V}}{1272727.27 \, \Omega} \]`

`\[ I \approx \frac{8000 \, \text{V}}{1.27 * 10^6 \, \Omega} \]`

`\[ I \approx 0.00629 \, \text{A} \]`

So, the current flowing through the silicon rod is approximately
`\(0.00629 \, \text{A}\).`

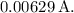
The complete question is:

What current flows through a 2.54 cm diameter rod of pure silicon that is 28.0 cm long, when 8.00 x 103 V is applied to it? The resistivity of silicon is 2300 Ωm.