Question

Attached below is my calculus question

(An inverted pyramid is being filled with water at a constant rate of..)

Thank you.

Answer 1

20.42 cm/s

Explanation:

You want to know the rate at which the water level is rising in an inverted pyramid with height 7 cm and square base 4 cm on a side, when the height of the water is 3 cm and the influx is 60 cc/s.

Surface area

When the height of the water is 3 cm, the side length of the square surface of the water is ...

(3 cm)(4/7) = 12/7 cm

Its area is then ...

A = s² = (12/7 cm)² = (144/49) cm²

Height

The rate of change of height is the rate of change of volume, divided by the surface area:

h' = (60 cm³/s)/(144/49 cm²) = (49·60/144) cm/s ≈ 20.42 cm/s

The level is rising at about 20.42 cm/s.

__

Additional comment

For b=4/7h, the volume formula becomes ...

V = 1/3(4/7h)²h = 16/147h³

h' = V'(49/(16h²)) = 60·49/144, as above

<95141404393>

Answer 2

20.42 cm/sec

Explanation:

The volume (V) of a square-based pyramid with perpendicular height h and base side b is given by:

`V=(1)/(3)b^2h`

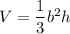
Given that b = 4 when h = 7, then:

`\begin{aligned}b:h&=4:7 \\\\(b)/(h)&=(4)/(7)\\\\b&=(4h)/(7)\end{aligned}`

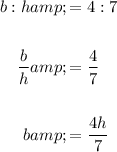
Substitute this into the volume equation so that we have an equation for V in terms of h:

`V=(1)/(3)\left((4h)/(7)\right)^2h`

`V=(1)/(3)\left((16h^2)/(49)\right)h`

`V=(16)/(147)h^3`

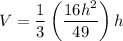
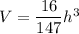
A derivative represents the rate of change of a function with respect to its independent variable. So, when something changes over time, the derivative is d/dt of that variable.

To determine the rate at which the water level is rising when the water level is 3 cm, we need to find an equation for dh/dt in terms of h.

Begin by differentiating volume (V) with respect to t by using the chain rule:

`\frac{\text{d}}{\text{d}t}\left(V\right)=\frac{\text{d}}{\text{d}t}\left((16)/(147)h^3\right)`

`\frac{\text{d}}{\text{d}t}\left(V\right)=(16)/(147)\cdot \frac{\text{d}}{\text{d}t}\left(h^3\right)`

`\frac{\text{d}V}{\text{d}t}=(16)/(147)\cdot \frac{\text{d}h}{\text{d}t}\cdot 3h^2`

`\frac{\text{d}V}{\text{d}t}=(48)/(147)h^2\cdot \frac{\text{d}h}{\text{d}t}`

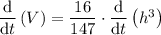
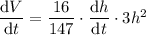
Given that the rate of change of volume (dV/dt)​ is 60 cubic centimeters per second, then:

`\frac{\text{d}V}{\text{d}t}=60`

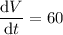
Substitute this into the equation:

`60=(48)/(147)h^2\cdot \frac{\text{d}h}{\text{d}t}`

Rearrange the equation to isolate dh/dt:

`(60\cdot 147)/(48h^2)= \frac{\text{d}h}{\text{d}t}`

`\frac{\text{d}h}{\text{d}t}=(735)/(4h^2)`

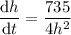
Now, we have the equation for the rate of change of the height of the inverted pyramid (dh/dt) in terms height (h).

To find the rate at which the water level (h) is rising when the water level is 3 cm, simply substitute h = 3 into dh/dt:

`\frac{\text{d}h}{\text{d}t}=(735)/(4(3)^2)`

`\frac{\text{d}h}{\text{d}t}=(735)/(4(9))`

`\frac{\text{d}h}{\text{d}t}=(735)/(36)`

`\frac{\text{d}h}{\text{d}t}=20.4166666...`

`\frac{\text{d}h}{\text{d}t}=20.42\;\sf cm/s\; (2\;d.p.)`

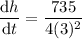
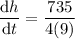
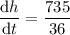
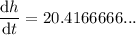
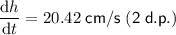
Therefore, the rate at which the water level (h) is rising is 20.42 cm/sec.