Question

Shown below is my calculus question, thank you.

Answer 1

• V = π/12h³
• 200/(169π) ≈ 0.3767 ft/min

Explanation:

You want the formula for the volume of a right circular cone with height equal to diameter, and you want the rate of change of height if the volume is increasing at 50 cfm when the height is 13 ft.

Volume

The radius is half the diameter, so for this cone it is half the height. The volume formula becomes ...

V = 1/3πr²h

V = 1/3π(h/2)²h

V = π/12h³ . . . . . . . formula for volume

Rate of change

The rate of change of volume is ...

V' = 3π/12h²h' = (π/4)h²h'

Then the rate of change of height is ...

h' = V'/(π/4h²) = 4V'/(πh²)

h' = 4(50 ft³/min)/(π(13 ft)²) = 200/(169π) ft/min ≈ 0.3767 ft/min

The height is increasing at the rate of about 0.3767 ft/min.

__

Additional comment

You may have noticed that the rate of change of height is the rate of change of volume divided by the area of the base. This will be the general case. (You don't need to go through the exercise of rewriting the volume formula.)

<95141404393>

Answer 2

`0.377 \sf \;(ft)/(min)`

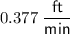
Explanation:

The volume (V) of a right circular cone with height h and radius of the base r is given by:

`V=(1)/(3)\pi r^2 h`

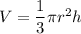
We are told that when gravel is being dumped from a conveyor belt, it forms a pile in the shape of a right circular cone whose base diameter and height are always equal. Therefore, we can rewrite the volume equation in terms of h only by substituting r = h/2 (since the radius is half the diameter):

`V=(1)/(3)\pi \left((h)/(2)\right)^2 h`

`V=(1)/(3)\pi \left((h^2)/(4)\right) h`

`V=(\pi)/(12) h^3`

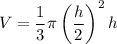
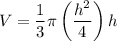
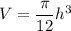
A derivative represents the rate of change of a function with respect to its independent variable. So, when something changes over time, the derivative is d/dt of that variable.

To determine how fast the height of the pile of gravel is increasing given its height, we need to find an equation for dh/dt in terms of h.

Begin by differentiating volume (V) with respect to t:

`\frac{\text{d}}{\text{d}t}\left(V\right)=\frac{\text{d}}{\text{d}t}\left((\pi )/(12)h^3\right)`

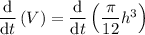
Take out the constant π/12:

`\frac{\text{d}}{\text{d}t}\left(V\right)=(\pi )/(12)\cdot \frac{\text{d}}{\text{d}t}\left(h^3\right)`

Differentiate using the chain rule:

`\frac{\text{d}V}{\text{d}t}=(\pi )/(12)\cdot 3h^2 \cdot \frac{\text{d}h}{\text{d}t}`

`\frac{\text{d}V}{\text{d}t}=(\pi h^2)/(4) \cdot \frac{\text{d}h}{\text{d}t}`

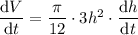
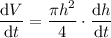
Given that the rate of change of volume (dV/dt)​ is 50 cubic feet per minute, then:

`\frac{\text{d}V}{\text{d}t}=50`

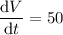
Substitute this into the equation:

`50=(\pi h^2)/(4) \cdot \frac{\text{d}h}{\text{d}t}`

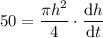
Rearrange the equation to isolate dh/dt:

`\frac{\text{d}h}{\text{d}t}=(200)/(\pi h^2)`

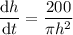
Now, we have the equation for the rate of change of the height of the pile of gravel (dh/dt) in terms of height (h).

To determine how fast the height of the pile of gravel is increasing when the pile is 13 feet high, simply substitute h = 13 into dh/dt:

`\frac{\text{d}h}{\text{d}t}=(200)/(\pi (13)^2)`

`\frac{\text{d}h}{\text{d}t}=(200)/(169\pi)`

`\frac{\text{d}h}{\text{d}t}=0.376698090...`

`\frac{\text{d}h}{\text{d}t}=0.377\; \sf ft/min\;(3\;s.f.)`

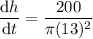
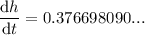
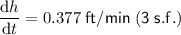
Therefore, the height of the pile of gravel is increasing at a rate of 0.377 feet per minute.