After solving \sqrt[6]{2x+1} + 3 = 0, the solution would be x = ?

Question

After solving
`\sqrt[6]{2x+1}` + 3 = 0, the solution would be x = ?

Answer 1

No solution

Explanation:

Given equation:

`\sqrt[6]{2x+1}+3=0`

To solve the given equation, begin by subtracting 3 from both sides of the equation:

`\begin{aligned}\sqrt[6]{2x+1}+3-3&=0-3\\\\\sqrt[6]{2x+1}&=-3\end{aligned}`

For the expression
`\sqrt[6]{2x+1}` to be defined, 2x + 1 should be non-negative. This means that
`\sqrt[6]{2x+1} \geq 0`.

Therefore,
`\sqrt[6]{2x+1}` cannot be equal to -3 for all real numbers.

So, there is no solution for
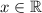`x \in \mathbb{R}`.