Question

You are given the following null and alternate hypotheses:

H0 : M = 525

H1 : M > 525

The test statistic for this hypothesis test is z0 = 2.35.

For this problem, use the provided Standard Normal Table (Z table). Determine the p-value for this test. Enter the p-value in the space below as a decimal rounded to four decimal places:

Answer 1

The p-value for the hypothesis test with
`\(H_0: M = 525\)` and
`\(H_1: M > 525\),` where the test statistic is
`\(z_0 = 2.35\)`, is approximately 0.0096, rounded to four decimal places.

To determine the p-value for the given test statistic
`\(z_0 = 2.35\)`, we can refer to the Standard Normal Table (Z table).

The null hypothesis
`\(H_0\)` states that the population mean
`(\(M\))` is equal to 525, and the alternate hypothesis
`\(H_1\)` states that
`\(M\)` is greater than 525.

The p-value is the probability of observing a test statistic as extreme as
`\(z_0\)` under the null hypothesis. Since
`\(H_1\)` is a right-tailed test (indicating greater than), we're interested in the area to the right of
`\(z_0\)` in the Z table.

Looking up
`\(z_0 = 2.35\)` in the Z table, we find the corresponding cumulative probability. The p-value is the probability of observing a z-score greater than 2.35.

From the Z table, we find that the cumulative probability for
`\(z_0 = 2.35\)` is approximately 0.9904.

Therefore, the p-value for this test is
`\(1 - 0.9904 = 0.0096\).`

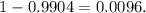
So, the p-value is 0.0096 (rounded to four decimal places).