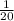Question

Bob and Rob write down letters from their names on 3 separate blank cards and shuffle them resulting in a pile of 6 cards. Their friend Robby then deals out 3 cards to Bob, placing them in front of him from left to right.

What is the probability that Bob is able to spell his name with the three cards?
What is the probability that he is able to spell Rob's name with the cards?
What is the probability that Bob is dealt out the cards so they spell out his name in the correct order?

Answer 1

The probability that Bob can spell his own name with three cards is 1/20. The probability of spelling Rob's name is also 1/20. The chance of spelling his name in order is also 1/20.

Let's break down the problem step by step.

1. Probability that Bob can spell his own name:

Bob has three cards out of six in the pile. The probability of getting the first letter of his name is 3/6, the probability of getting the second letter is 2/5, and the probability of getting the third letter is 1/4 (since there are no replacement and the cards are not returned to the pile).

Therefore, the probability that Bob can spell his own name is:

`\( (3)/(6) * (2)/(5) * (1)/(4) = (1)/(20) \)`

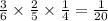
2. Probability that Bob can spell Rob's name:

Similarly, the probability that Bob can spell Rob's name is calculated using the same logic. Since the letters in Bob and Rob are different, the probability would be:

`\( (3)/(6) * (2)/(5) * (1)/(4) = (1)/(20) \)`

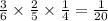
3. Probability that Bob is dealt the cards to spell out his name in the correct order:

In this case, there is only one way for Bob to spell his name correctly, so the probability is the same as the probability of spelling his name:

`\( (1)/(20) \)`

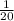
In summary:

1. Probability that Bob can spell his own name:
`\( (1)/(20) \)`

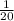
2. Probability that Bob can spell Rob's name:
`\( (1)/(20) \)`

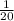
3. Probability that Bob is dealt the cards to spell out his name in the correct order:
`\( (1)/(20) \)`