The equation representing the direct variation between Jalen's mobile phone cost
 and the number of minutes
and the number of minutes
 The constant of variation is 0.05, showing a proportional relationship.
The constant of variation is 0.05, showing a proportional relationship.
The relationship between the cost
 and the number of minutes
and the number of minutes
 is said to vary directly if it can be expressed in the form
is said to vary directly if it can be expressed in the form
 where
where
 is the constant of proportionality or constant of variation.
is the constant of proportionality or constant of variation.
Given the information in the table, let's find the constant of variation
 :
:
1. For the first data point (150 minutes, $7.50):
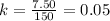
2. For the second data point (220 minutes, $11.00):

3. For the third data point (250 minutes, $12.50):
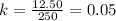
4. For the fourth data point (275 minutes, $13.75):
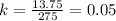
Since
 is consistently 0.05 for all data points, the equation representing the variation is
is consistently 0.05 for all data points, the equation representing the variation is
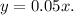
Therefore, among the given options, the correct equation representing the variation is:
![\[ y = 0.05x \]](https://img.qammunity.org/2024/formulas/mathematics/college/86fj59q33eov15fn6utee0fiyq29gw434k.png)
Now, let's address the statement:
![\[ (10x)/(3y) = 1 \]](https://img.qammunity.org/2024/formulas/mathematics/college/j2jh8upkl6sxz6whyd0tsvu8d64noctsqo.png)
By rearranging this equation, we get:
![\[ (10)/(3) = (x)/(y) \]](https://img.qammunity.org/2024/formulas/mathematics/college/a3t7rv83egoc86zlz7329w124avy70f13u.png)
This implies that the constant of variation
 is
is
 , which is not the same as the constant of variation found earlier
, which is not the same as the constant of variation found earlier
 . Therefore, the statement "The constant of variation is the same for the graph and the equation" is false.
. Therefore, the statement "The constant of variation is the same for the graph and the equation" is false.
So, the correct statement is: The constant of variation cannot be compared because the equation is nonproportional.