Question

What is the value of x if the area of the trapezoid is 306 square units?

Answer 1

The height
`(\(x\))` of the trapezoid is 17 units. Given bases of 15 units and 21 units, the area of 306 square units is achieved using the formula
`\(A = (1)/(2)(a + b)h\).`

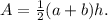
The area of a trapezoid can be calculated using the formula
`\(A = (1)/(2)(a + b)h\),` where
`\(a\)` and
`\(b\)` are the lengths of the bases and
`\(h\)` is the height. In this case, the area is given as 306 square units, and one base (a) is 15 units, while the other base (b) is 21 units.

To find the height
`(\(h\))`, we can rearrange the formula to solve for \(h\):

`\[h = (2A)/(a + b)\]`

Substituting the given values into the formula, we get:

`\[h = (2 * 306)/(15 + 21)\]`

Simplifying the expression:

`\[h = (612)/(36) = 17\]`

Therefore, the height
`(\(x\))` of the trapezoid is 17 units. This means that if the bases of the trapezoid are 15 units and 21 units, the height required to yield an area of 306 square units is 17 units. This calculation illustrates how the formula for the area of a trapezoid can be employed to determine a specific dimension (height) when the area and the lengths of the bases are known.

The probable question maybe:

Statement: The area of a trapezoid is 306 square units.

Question: If the bases of the trapezoid are 15 units and 21 units, what is the length of the height (x) of the trapezoid?