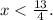The solution to the inequality
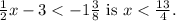
Sure, let's solve the inequality:
![\[ (1)/(2)x - 3 < -1(3)/(8) \]](https://img.qammunity.org/2024/formulas/mathematics/college/j5mb4svtl6rfap69l5i6wfwotjrlmgjoez.png)
First, let's simplify the right side of the inequality:
![\[ -1(3)/(8) = -(11)/(8) \]](https://img.qammunity.org/2024/formulas/mathematics/college/iwu65vg3pg7ydcabm21sxynqxnu1jb4e4f.png)
Now, rewrite the inequality:
![\[ (1)/(2)x - 3 < -(11)/(8) \]](https://img.qammunity.org/2024/formulas/mathematics/college/5dmpgjqyzkau7uysnv50y5whm0gq0adnbr.png)
Add 3 to both sides to isolate the term with \(x\):
![\[ (1)/(2)x < -(11)/(8) + 3 \]](https://img.qammunity.org/2024/formulas/mathematics/college/6d2k7r764he67oivxgf1l4mescz78sww02.png)
Combine the terms on the right side:
![\[ (1)/(2)x < (13)/(8) \]](https://img.qammunity.org/2024/formulas/mathematics/college/lawm524okauejbcmrq6jaj55w5ckpsz5ns.png)
Now, multiply both sides by 2 to solve for \(x\):
![\[ x < (13)/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/college/1bvirntve6x33zoq0sthav8sh4tm4anc5i.png)
So, the solution to the inequality is