Question

Which graph best represents this system of equations and its solutions?

-4y=-8x-16
y=-1/5x-2/5

Answer 1

Lines with slopes 2 and -1/5 intersect at (-20/11, 8/11).

The first equation, $-4y = -8x - 16$, can be rewritten as $y = 2x + 4$. This is the equation of a line with a slope of $2$ and a y-intercept of $4$.

The second equation, $
`y = -(1)/(5)x - (2)/(5)` $, is the equation of a line with a slope of $
`-(1)/(5)` $ and a y-intercept of $
`-(2)/(5)`$.

The slopes of the two lines are negative inverses of each other, so the lines are perpendicular.

The solution to the system of equations is the point where the two lines intersect. We can find this point by setting the two equations equal to each other:

$2x + 4 =
`-(1)/(5)x - (2)/(5)$`

Solving for $x$, we get $x =
`-(20)/(11)$.`

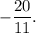
Substituting $
`-(20)/(11)$ for $x$ in either of the original equations, we get $y = (8)/(11)$.`

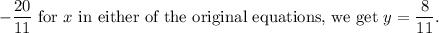
The solution to the system of equations is
`$\boxed{\left( -(20)/(11), (8)/(11) \right)}$.`