Question

Higher Order Thinking Write an indirect proof about the given conditional using either contradiction or contrapositive. What is an advantage of the method you chose?

Answer 1

Assume
`\( n \)` is odd when
`\( n^2 \)` is even. Squaring
`\( n \)` yields
`\( n^2 = 2(2k^2 + 2k) + 1 \)`, contradicting evenness. Thus, if
`\( n^2 \)` is even,
`\( n \)` must be even.

Let's consider the given conditional statement: "If
`n^2`is an even integer, then n must be an even integer." We want to prove this indirectly using either contradiction or contrapositive. In this case, I'll choose to prove it by contradiction.

Indirect Proof (Proof by Contradiction):

Assume for the sake of contradiction that
`\( n \)` is an odd integer when
`\( n^2 \`) is an even integer.

1. Let
`\( n \)` be an odd integer, so
`\( n = 2k + 1 \)` for some integer
`\( k \).`

2. Square
`\( n \):`
`\( n^2 = (2k + 1)^2 = 4k^2 + 4k + 1 \).`

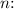
3. Notice that
`\( n^2 \)` can be expressed as
`\( 2(2k^2 + 2k) + 1 \),` which is the form of an odd integer.

This contradicts our initial assumption that
`\( n^2 \)` is an even integer. If
`\( n^2 \)` were even, it should be expressible as
`\( 2m \)` for some integer
`\( m \)` , but we've shown that
`\( n^2 \)` is in the form of
`\( 2(2k^2 + 2k) + 1 \),` which is odd.

Therefore, our assumption that
`\( n \)` is an odd integer when
`\( n^2 \`) is even leads to a contradiction. By the principle of proof by contradiction, we conclude that the original statement is true: "If
`\( n^2 \)`is an even integer, then
`\( n \)` must be an even integer."

Advantage of Proof by Contradiction:

One advantage of using proof by contradiction is its simplicity in structure and clarity in reasoning. By assuming the negation of the statement to be proved and showing that this assumption leads to a logical contradiction, we establish the truth of the original statement. This method often provides a direct and concise path to the conclusion, making it an efficient and effective proof strategy. Additionally, proof by contradiction is a versatile approach that can be applied to a wide range of mathematical statements.