Question

Find the answer, cause i have a test on monday 4th december

Answer 1

For p = 2.5, H is approximately
`\( (5)/(8) \)`, and for H = 27, p is 3. The constant of proportionality is k = 5.

In an inversely proportional relationship, the formula is
`\(H = (k)/((2p - 3)^3)\)`, where j is the constant of proportionality.

Given that H = -5 when p = 1, we can determine k:

`\[ -5 = (k)/((2(1) - 3)^3) \]`

Solving for k, we find k = 5.

Now, for part (i) when p = 2.5, we substitute into the formula:

`\[ H = (5)/((2(2.5) - 3)^3) \]`

After calculations, H is approximately
`\( (5)/(8) \).`

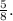
For part (ii), when H = 27, we set up the equation:

`\[ 27 = (5)/((2p - 3)^3) \]`

Solving for p, we find p = 3.

In summary, for p = 2.5, H is approximately
`\( (5)/(8) \)`, and for H = 27, p is 3. The constant of proportionality is k = 5.

The probable question may be:

(b) If H is inversely proportional to (2p-3)^3 and

H= -5 when p=1, find

(i) the value of H when p=2.5

(ii)the value of p when H= 27