Question

I have no clue how to do this because my rate law expression does not include the Iron needed for part c.

Answer 1

The rate law expression for the reaction is Rate = k[MnO4-]. The calculated rate constant (k) is
`1.248*10^(-2) min^{-1.` To achieve a desired rate of
`2.0*10^{-3`M/min with [MnO4-] of 0.040 M and [H+] of 0.100 M, [Fe2+] needs to be 0.160 M.

To determine the rate law expression for the reaction of iron (II) with permanganate in acidic solution, we analyze the given data.

Comparing Trial 1 and Trial 2, the concentration of H+ is doubled while the concentrations of Fe2+ and MnO4- remain the same, but the rate does not change significantly.

Therefore, H+ does not appear to affect the rate, suggesting zero order with respect to H+ ions.

Comparing Trial 1 and Trial 3, doubling the concentration of MnO4- doubles the rate, indicating first-order with respect to MnO4-.

From Trial 1 and Trial 4, increasing the concentration of Fe2+ by a factor of 3 changes the rate insignificantly, suggesting it is also not affecting the rate, or zero order with respect to Fe2+ ions.

Therefore, the rate law is Rate = k[MnO4-].

To calculate the rate constant (k), we use the data from Trial 1 where the rate is
`3.12*10^{-4`M/min and the concentration of MnO4- is 0.025 M.

Substituting into the rate law gives k = rate/[MnO4-] = (
`3.12*10^{-4`M/min) / 0.025 M, which results in k =
`1.248*10^(-2 )min^{-1`

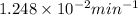
For question (c), we have the rate law and k, and we need the concentration of Fe2+ that would give a rate of
`2.0*10^{-3`M/min

The equation would be
`2.0*10^{-3`M/min =
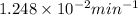`1.248*10^(-2 )min^{-1` [Fe2+], solving for [Fe2+] gives [Fe2+] = 0.160 M.

The probable question may be:

Use the data of the balanced chemical reaction, between iron (II) and permanganate in acidic solution, to answer the following questions (a-c):

5 Fe^{2+} (aq) + MnO_4^- (aq) + 8 H^+ (aq) → 5 Fe^{3+} (aq) + Mn^{2+} (aq) + 4 H_2O (l)

Trial [Fe^{2+}] [MnO_4^-] [H^+] rate

1 0.010 M 0.025 M 0.050 M 3.12x10^{-4} M/min

2 0.010 M 0.025 M 0.100 M 3.04x10^{-4} M/min

3 0.010 M 0.050 M 0.050 M 6.31x10^{-4} M/min

4 0.030 M 0.025 M 0.100 M 2.71x10^{-4} M/min

a. Determine the rate law expression of the reaction

b. Calculate k

c. What [Fe2+] is required to achieve a rate of 2.0 x 10-3 M/min when [MnO4] = 0.040 M and [H+] = 0.100 M?