Answer:
See Below.
Explanation:
Please refer to the attachment below.
Essentially, we want to prove that AE bisects ∠A.
Statements: Reasons:
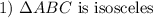 Given
Given
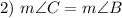 Isosceles Triangle Theorem
Isosceles Triangle Theorem
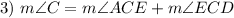 Angle Addition
Angle Addition
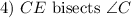 Given
Given
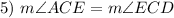 Definition of Bisector
Definition of Bisector
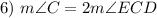 Substitution
Substitution
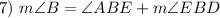 Angle Addition
Angle Addition
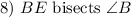 Given
Given
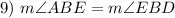 Definition of Bisector
Definition of Bisector
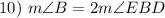 Substitution
Substitution
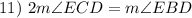 Substitution
Substitution
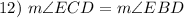 Division Property of Equality
Division Property of Equality
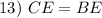 Isosceles Triangle Theorem
Isosceles Triangle Theorem
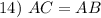 Isosceles Triangle Theorem
Isosceles Triangle Theorem
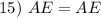 Reflexive Property
Reflexive Property
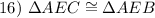 SSS Congruence
SSS Congruence
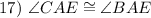 CPCTC
CPCTC
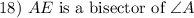 Converse of Bisector
Converse of Bisector