The equation of the line passing through the points (-4, 0) and (2, 2) in point-slope form is
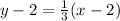 .
.
The figure in the image is a graph of a linear function.
The equation of a line point-slope form is expressed as:
y - y₁ = m( x + x₁ )
Where x₁ and y₁ are the coordinates of a point and m is the slope.
From the graph, the passes through the points (-4, 0) and (2, 2).
First, we determine the slope (m):
Slope (m) = ( change in y ) / ( change in x )
Slope (m) = ( y₂ - y₁ ) / ( x₂ - x₁ )
Slope (m) = ( 2 - 0 ) / ( 2 - (-4) )
Slope (m) = ( 2 - 0 ) / ( 2 + 4 )
Slope (m) = 2 / 6
Slope (m) = 1/3
Now, plug the slope m = 1/3 and point (2,2) into the point-slope form:
y - y₁ = m( x + x₁ )
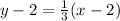
Therefore, the equation of the line is
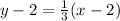 .
.