Question

In this figure, DC=2.8, and BC=9.3.

What is the length of AC?

Enter your answer rounded to the nearest tenth in the box.

Answer 1

5.1 units

Explanation:

• In this figure, DC=2.8, and BC=9.3. What is the length of AC? Enter your answer rounded to the nearest tenth in the box.

triangle ACD is similar to triangle ABC, answer and solution in the figure

Answer 2

The length of AC = 5.102 units. .

How to solve

Using the theorem of similar right triangles, we have

Recall, that the theorem of similar right triangles states that if an angle in one right triangle is equal to an angle in another, and their hypotenuses are proportional, they're similar.

DC/AC = BC/AC

Cross multiply

`AC^2 = DC * BC`

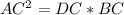
Substitute the given values

`AC^2 = 2.8 * 9.3`

`AC^2 = 26.04`

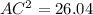
We expand using the square.

AC =
`\sqrt26.04`

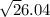
Therefore, it can be seen that the length of AC = 5.1 units.