Question

A line has equation y = k, where k is a constant. For which values of k does the line not intersect the circle with equation x x y y    2233 2 04.

Answer 1

The line
`\(y = k\)` does not intersect the circle
`\(x^2 + y^2 - 2x - 3y - 4 = 0\)` when
`\(k < -1\)` or
`\(k > 5\)`, as determined by the discriminant of the quadratic equation derived from the circle.

To find the values of
`\( k \)` for which the line
`\( y = k \)` does not intersect the circle with equation
`\( x^2 + y^2 - 2x - 3y - 4 = 0 \)`, we need to substitute
`\( y = k \)` into the circle equation and solve for
`\( x \).`

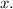
The circle equation is
`\( x^2 + y^2 - 2x - 3y - 4 = 0 \).` Substitute
`\( y = k \)\\`

`\[ x^2 + k^2 - 2x - 3k - 4 = 0 \]`

Now, rearrange the terms and express it as a quadratic equation:

`\[ x^2 - 2x + k^2 - 3k - 4 = 0 \]`

For the line
`\( y = k \)` not to intersect the circle, the discriminant of this quadratic equation
`(\( b^2 - 4ac \))` must be negative.

The discriminant is given by
`\( \Delta = (-2)^2 - 4(1)(k^2 - 3k - 4) \)`:

`\[ \Delta = 4 - 4(k^2 - 3k - 4) \]`

Expand and simplify:

`\[ \Delta = 4 - 4k^2 + 12k + 16 \]`

Now, set the discriminant less than zero:

`\[ 4 - 4k^2 + 12k + 16 < 0 \]`

Combine like terms:

`\[ -4k^2 + 12k + 20 < 0 \]`

Divide by -4 to simplify:

`\[ k^2 - 3k - 5 > 0 \]`

Now, factor the quadratic expression:

`\[ (k - 5)(k + 1) > 0 \]`

The critical points are
`\( k = -1 \)` and
`\( k = 5 \).` Test intervals to determine when the expression is positive:

- When
`\( k < -1 \)\\` Both factors are negative, so the expression is positive.

- When
`\( -1 < k < 5 \)` : The factor
`\( (k + 1) \)` is positive, and
`\( (k - 5) \)` is negative, so the expression is negative.

- When
`\( k > 5 \)` : Both factors are positive, so the expression is positive.

Therefore, the values of
`\( k \)` for which the line
`\( y = k \)` does not intersect the circle are
`\( k < -1 \) and \( k > 5 \).`