The equation of the ellipse is (x^2/64) + (y^2/81) = 1.
The equation of an ellipse in standard form is given by x^2/a^2+y^2/b^2=1, where a and b are the semi-major and semi-minor axes, respectively.
In the provided information, the ellipse has foci at (0, -9) and two vertices at (-8, 0). The distance between the center and each focus is the value of c, where c is related to a, b, and c by the equation c^2=a^2-b^2. The distance between the center and each vertex is a.
From the given information, we can determine that c=9 (since the foci are at (0, -9)), and a=8 (since the vertices are at (-8, 0)). Using the relationship c^2=a^2-b^2, we can solve for b. Substituting the known values, we find that
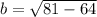
Therefore, the equation of the ellipse is (x^2/64) + (y^2/81) = 1. This form ensures that the ellipse is centered at the origin, with semi-major axis a=8 and semi-minor axis b=3, meeting the criteria of the provided properties.