Question

Evaluate the triple integral ∭ₑ z dV, where E is enclosed by the paraboloid z= x² + y² and the plane z=4.

Answer 1

The value of the triple integral ∭ₑ z dV, where E is enclosed by the paraboloid z=x^2 +y^2 and the plane z=4, is 32π/3.

The given triple integral ∭ₑ z dV involves evaluating the function z over a region E enclosed by the paraboloid z=x^2 +y^2 and the plane z=4. To compute this, we need to set up the limits of integration.

Firstly, the paraboloid z=x^2 +y^2 intersects with the plane z=4 at z=4. Therefore, the limits for z are from 0 to 4.

For x and y, we need to consider the projection of the region E onto the xy-plane. Since the paraboloid is symmetric about the z-axis, we can use polar coordinates. The limits for r (radial distance) are from 0 to
`√(4-z)` , where z varies from 0 to 4.The triple integral is then expressed as
`\int\limits^4_0`
`\int\limits^2_0`
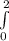
`\int\limits^4_0`r⋅zdrdθdz. Evaluating this expression yields the result of 32π/3, representing the volume under the paraboloid and above the plane within the specified limits.