Question

Use spherical coordinates. Evaluate Triple Integral (E) of y² dV, Where E is the solid hemisphere x²+y²+z² (equal or less than) 9, z (equal or greater than) 0.

Answer 1

The value of the triple integral
`\int\int\int_E y^2` dV is 27π/2.

let's evaluate the triple integral:

`\int\int\int_E y^2` dV

where E is the solid hemisphere
`x^2 + y^2 + z^2` ≤ 9 and z ≥ 0. We'll use spherical coordinates to solve this problem.

Define the bounds in spherical coordinates.

We know that
`x^2 + y^2 + z^2 = \rho^2`, where ρ is the radial distance. The constraint z ≥ 0 implies that φ (the angle with the positive z-axis) ranges from 0 to π/2. The bounds for θ (the azimuthal angle) are 0 to 2π, as we want to integrate over the entire hemisphere. Therefore, the bounds are:

0 ≤ ρ ≤ 3 (since the radius of the hemisphere is 3)

0 ≤ φ ≤ π/2

0 ≤ θ ≤ 2π

Substitute
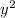`y^2` with its representation in spherical coordinates.

In spherical coordinates, y = ρ sin(φ) cos(θ). Therefore,
`y^2 = \rho^2 sin^2(\theta)`
`cos^2`(θ).

Set up the integral.

The integral now looks like:

∭_E
`\rho^4 sin^2(\theta) cos^2(\theta)`dV

We can use the Jacobian of spherical coordinates to convert dV:

dV =
`\rho^2` sin(φ) dρ dφ dθ

Evaluate the integral.

`\int_0^((2\pi)) \int_0^((\pi/2)) \int_0^3 \rho^6 sin^3(\phi) cos^2(\theta) d\rho d\phi d\theta`

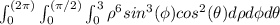
We can separate the variables and integrate:

`\int_0^((2\pi)) d\theta \int_0^((\pi/2)) sin^3(\phi) d\phi \int_0^3 \rho^6 cos^2(\theta) d\rho`

The integrals of θ and
`cos^2`(θ) are straightforward:

2π
`\int_0^((\pi/2)) sin^3(\phi) d\phi \int_0^3 \rho^6 d\rho`

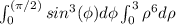
The integral of
`sin^3`(φ) can be solved using integration by parts:

2π (1/4 - 1/8)
`\int_0^3 \rho^6` dρ

Simplifying the expression:

π/2
`\int_0^3 \rho^6` dρ

Finally, evaluating the last integral:

(π/2) * (1/7) *
`3^7` = 27π/2

Therefore, the triple integral
`\int\int\int_E y^2` dV equals 27π/2.