1.
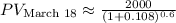
2.
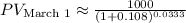
3.
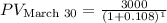
To calculate the present value of future cash flows, you can use the formula:
![\[ PV = (FV)/((1 + r)^n) \]](https://img.qammunity.org/2024/formulas/business/high-school/n1vup920g0tri5e81rdg0g91f96x4pczqq.png)
Where:
- \( PV \) is the present value,
- \( FV \) is the future value (cash flow),
- \( r \) is the interest rate per period,
- \( n \) is the number of periods.
Let's calculate the present values for each date:
1. March 18:
![\[ PV_{\text{March 18}} = \frac{2000}{(1 + 0.108)^{(18)/(30)}} \]](https://img.qammunity.org/2024/formulas/business/high-school/c2wjlveywz0rhkc02w36segijziu7dqw8p.png)
2. March 1:
![\[ PV_{\text{March 1}} = \frac{1000}{(1 + 0.108)^{(1)/(30)}} \]](https://img.qammunity.org/2024/formulas/business/high-school/ws333bilstbleq14sq8yoc6wy20s3hwioh.png)
3. March 30:
![\[ PV_{\text{March 30}} = \frac{3000}{(1 + 0.108)^{(30)/(30)}} \]](https://img.qammunity.org/2024/formulas/business/high-school/ec3ek47kuqysnrkpakt7o3fb6wb89r1lsh.png)
Now, calculate the values:
1.

2.
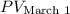
3.
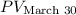
Please note that the time is expressed in years, and the number of days is relative to a 30-day month.