Question

Let PM be the perpendicular from the point P(1,2,3) to XY-plane. If OP makes an angle θ with the positive direction of the Z-axies and OM makes an angle Φ with the positive direction of X-axis, where O is the origin, then find θandΦ.

Answer 1

The angle
`\( \theta \)` between the vector OP and the positive Z-axis is
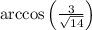`\(\arccos\left((3)/(√(14))\right)\)`, and the angle
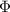`\( \Phi \)` with the positive X-axis is
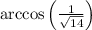`\(\arccos\left((1)/(√(14))\right)\)` for the point P(1, 2, 3).

To find the angles θ and Φ, we can use the coordinates of the point P(1, 2, 3) and the definition of angles in three-dimensional space.

Let's start by finding the components of the vector OP (vector from the origin O to point P):

`\[ \vec{OP} = \langle x_P, y_P, z_P \rangle = \langle 1, 2, 3 \rangle \]`

The angle
`\( \theta \)` with the positive direction of the Z-axis can be found using the z-component of the vector OP:

`\[ \cos(\theta) = \frac{z_P}{|\vec{OP}|} \]\[ \cos(\theta) = (3)/(√(1^2 + 2^2 + 3^2)) \]\[ \cos(\theta) = (3)/(√(14)) \]\[ \theta = \arccos\left((3)/(√(14))\right) \]`

Similarly, the angle
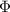`\( \Phi \)` with the positive direction of the X-axis can be found using the x-component of the vector OP:

`\[ \cos(\Phi) = \frac{x_P}{|\vec{OP}|} \]\[ \cos(\Phi) = (1)/(√(14)) \]\[ \Phi = \arccos\left((1)/(√(14))\right) \]`

So,
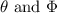`\( \theta \) and \( \Phi \)` are given by the arccosine of
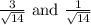`\((3)/(√(14))\) and \((1)/(√(14))\)`, respectively. You can use a calculator to find the numerical values for these angles.