For the given equations to share a common root, the exhaustive set for a is
![\( a \in (-\infty, -2] \cup [2, +\infty) \)](https://img.qammunity.org/2024/formulas/mathematics/high-school/7dxl40g9grlf4utdyt4lfpggjwf8dftig2.png) , where
, where

Let's work through this:
Given equations:
1.
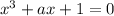
2.
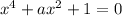
If these equations have a common root, let's say x = r, then substituting x = r into both equations should satisfy both.
1. For
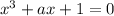 :
:
![\[ r^3 + ar + 1 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nib71vb295xgo8f9iqrbn9bnm33x1ehkz9.png)
2. For
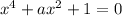 :
:
![\[ r^4 + ar^2 + 1 = 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5ua88mku40oqm1hrlhdtlvkv2a360r9anv.png)
Now, let's consider the discriminants of the above quadratic equations.
1. Discriminant of
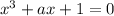 is
is

2. Discriminant of
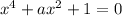 is
is

For real roots, the discriminant must be greater than or equal to zero. Therefore:
![\[ a^2 - 4 \geq 0 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7agofb3hfn4tcbbsr1ke2prj4pzvp55dil.png)
Solving for a :
![\[ a^2 \geq 4 \\\\\[ |a| \geq 2 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/zx60qifybr73ezf5pq7ckzf2k2mkgrnfc3.png)
So, any real value of a such that |a|
 2 would satisfy the condition that the two equations have a common root. The exhaustive set of values for a is
2 would satisfy the condition that the two equations have a common root. The exhaustive set of values for a is
![\( (-\infty, -2] \cup [2, +\infty) \)](https://img.qammunity.org/2024/formulas/mathematics/high-school/th0epmsual6dp5vx821bgozq69fknf5ipk.png) .
.