Question

pollution and altitude: in a random sample of cars driven at low altitudes, of them exceeded a standard of grams of particulate pollution per gallon of fuel consumed. in an independent random sample of cars driven at high altitudes, of them exceeded the standard. can you conclude that the proportion of high-altitude vehicles exceeding the standard differs from the proportion of low-altitude vehicles exceeding the standard? let denote the proportion of low-altitude vehicles exceeding the standard and denote the proportion of high-altitude vehicles exceeding the standard. use the level of significance and the -value method with the ti-84 plus calculator.

Answer 1

Perform a two-proportion z-test using sample proportions of vehicles exceeding pollution standards at low and high altitudes. Compare the p-value to the chosen significance level (e.g., 0.05) for a conclusion on whether proportions differ. Use a TI-84 Plus calculator for calculations.

To determine whether the proportion of high-altitude vehicles exceeding the pollution standard differs from the proportion of low-altitude vehicles exceeding the standard, you can perform a hypothesis test for the difference between two proportions. Let
`P_1` be the proportion of low-altitude vehicles exceeding the standard, and
`p _2` be the proportion of high-altitude vehicles exceeding the standard.

The null hypothesis (
`H_0` ) and alternative hypothesis (
`H _a`) can be stated as follows:

`H_0:p_1 = p_2`

`H_0:p_1` ≠
`p_2`

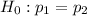
​This is a two-sided test because you want to determine if there is a significant difference in either direction.

Next, you need to choose the level of significance (α), which is the probability of rejecting a true null hypothesis. Common choices are 0.05, 0.01, or 0.10.

Let's assume α=0.05 for this example.

Now, you can perform the hypothesis test using the z-test for the difference between two proportions. The formula for the test statistic is:

`z = \frac{\bar p_1 - \bar p_2}{\sqrt{p(1-p)((1)/(n_1) -(1)/(n_2) )} }`

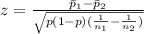
where
`\bar p_1`and
`\bar p_2`are the sample proportions, p is the combined sample proportion, and
`n_1`and
`n _2` are the sample sizes.

Now, calculate the z-score and find the corresponding p-value. You can use a calculator like the TI-84 Plus for these calculations.

Once you have the p-value, compare it to the chosen level of significance (α):

If p-value <α, reject the null hypothesis.

If p-value ≥α, fail to reject the null hypothesis.

If you have the p-value and need assistance interpreting it or calculating the z-score with the TI-84 Plus, please provide the sample sizes and sample proportions, and I can guide you through the process.