Question

Described provide counterexamples to a continuous function preserving almost uniform convergence and convergence in measure?

Answer 1

Continuous functions do not necessarily preserve almost uniform convergence or convergence in measure. Counterexamples can be constructed using functions like x^2 and sin(2πx) on the interval [0, 1].

Counterexample for almost uniform convergence:

Consider the functions
`$f(x) = x^2$ and $g(x) = \sin(2\pi x)$` on the interval
`$[0, 1]$`. Both f and g are continuous on [0, 1]. However, they do not converge almost uniformly on [0, 1].

To see this, let
`$\epsilon = 0.1$`. For any set E of positive Lebesgue measure, there exists a sequence of functions
`$(f_n)$` that converges pointwise to f on E such that

`$$\limsup_(n \to \infty) \int_E |f_n(x) - f(x)| \, dx > \epsilon.$$`

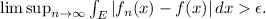
This shows that f does not converge almost uniformly to g on [0, 1].

Counterexample for convergence in measure:

Consider the same functions
`$f(x) = x^2$ and $g(x) = \sin(2\pi x)$` on the interval [0, 1]. Both f and g are continuous on [0, 1]. However, they do not converge in measure on [0, 1].

To see this, let
`$\epsilon` = 0.1. There exists a sequence of functions
`$(f_n)$` that converges pointwise to f on [0, 1] such that

`$$\lim_(n \to \infty) m(\x \in [0, 1] : ) > 0.$$`

This shows that
`$f$` does not converge in measure to
`$g$` on [0, 1].