Final Answer:
The flowchart proof demonstrates that, given start
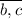 is parallel to
is parallel to
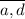 , we can conclude that
, we can conclude that
 is congruent to
is congruent to
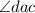 , and
, and
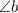 is congruent to
is congruent to
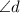 . This is supported by the fact that
. This is supported by the fact that
 is congruent to
is congruent to
 , and triangles
, and triangles
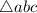 and
and
 are congruent.
are congruent.
Step-by-step explanation:
The given information states that
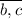 is parallel to
is parallel to
 From this, we can deduce that alternate interior angles are congruent. Therefore,
From this, we can deduce that alternate interior angles are congruent. Therefore,
 is congruent to
is congruent to
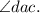 This is the first key step in establishing the congruence between the two triangles.
This is the first key step in establishing the congruence between the two triangles.
The second piece of information is that
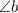 is congruent to
is congruent to
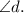 This is a consequence of the fact that corresponding angles formed by the parallel lines
This is a consequence of the fact that corresponding angles formed by the parallel lines
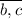 and
and
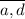 are congruent. This establishes the second angle congruence.
are congruent. This establishes the second angle congruence.
Now, with the two angles and a side
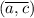 being congruent, we can apply the Angle-Side-Angle (ASA) congruence criterion to prove that
being congruent, we can apply the Angle-Side-Angle (ASA) congruence criterion to prove that
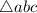 is congruent to
is congruent to
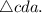 This is due to the fact that a triangle is congruent to another if they have two corresponding angles and the included side congruent. Therefore, the triangles
This is due to the fact that a triangle is congruent to another if they have two corresponding angles and the included side congruent. Therefore, the triangles
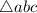 and
and
 are congruent, and the proof is complete.
are congruent, and the proof is complete.