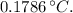The calculated change in temperature
 is approximately
is approximately
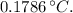
Determining the temperature in a wire from the given potential difference (V = 5.6V) and current (I = 0.04A) involves understanding the relationship between electrical power, resistance, and temperature change.
The power dissipated in the wire can be calculated using the formula P = IV, where P is power, \(I\) is current, and \(V\) is potential difference.
![\[ P = (0.04\,A) * (5.6\,V) = 0.224\,W \]](https://img.qammunity.org/2024/formulas/biology/college/g487aen6xhpqsum2nj1yj7cpelfnhmpxya.png)
Next, we need to consider the power equation
 , where \(R\) is resistance.
, where \(R\) is resistance.
Rearranging for resistance,
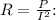
![\[ R = (0.224\,W)/((0.04\,A)^2) = 140\,\Omega \]](https://img.qammunity.org/2024/formulas/biology/college/65ul9lfxoirwym9sazhbi8vqsy2w506mm0.png)
Now, the temperature change
 can be determined using the relationship between power, resistance, and temperature change given by
can be determined using the relationship between power, resistance, and temperature change given by

![\[ \Delta T = (P)/(I^2R) = (0.224\,W)/((0.04\,A)^2 * 140\,\Omega) \]](https://img.qammunity.org/2024/formulas/biology/college/ke9en71kd2jvx2zom6rzosp4hqycw8kiwz.png)
The given expression is for calculating the change in temperature
 using the formula
using the formula
 , where (P) is the power, (I) is the current, and (R) is the resistance.
, where (P) is the power, (I) is the current, and (R) is the resistance.
Substitute the provided values into the formula:
![\[ \Delta T = (0.224\,W)/((0.04\,A)^2 * 140\,\Omega) \]\\ \\\Delta T = (0.224\,W)/(0.000064\,A^2 * 140\,\Omega) \]](https://img.qammunity.org/2024/formulas/biology/college/ibaufig8d6qv29x1tpoo3e0sx1dowrmruc.png)
Simplify the expression:
![\[ \Delta T = (0.224\,W)/(0.00896\,A^2 * 140\,\Omega) \]\\\\\Delta T \approx (0.224\,W)/(1.2544\,A^2) \]\\\\\Delta T \approx 0.1786\, ^\circ C \]](https://img.qammunity.org/2024/formulas/biology/college/oeoklqhm5extrf79ij3w5njzdhyjpbdhno.png)
Therefore, The calculated change in temperature
 is approximately
is approximately