Question

According to a study I just made up, the probability a randomly selected individual will not cover their mouth when sneezing is 20 %. Suppose you sit in public and record the sneezing habits of 10 randomly selected people.

Define the random variable associated with the experiment of recording the sneezing habits of 10 randomly selected people by giving both its definition and its probability mass function.

Answer 1

Random Variable: X represents the number of people out of 10 who don't cover their mouth when sneezing. PMF: P (X=k) =(10/k) .
`0.2^(k)` .
`0.8^(10-k)` .

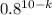Certainly! Let's define a random variable for this experiment.

Let X be the random variable representing the number of people out of the 10 randomly selected individuals who do not cover their mouth when sneezing.

Now, let's define the probability mass function (PMF) for X. The PMF gives the probability of each possible value of the random variable.

If the probability that a randomly selected individual does not cover their mouth when sneezing is 20%, then the probability of an individual covering their mouth is 1−0.2=0.8.

The PMF is given by the binomial distribution formula:

P(X=k)= (
`(n)/(k)`).
`p^(k)` .
`(1-p)^(n-k)`

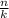Where:

n is the number of trials (number of people observed, which is 10 in this case),

k is the number of successes (number of people not covering their mouth when sneezing),

p is the probability of success on a single trial.

In this case:

n=10 (10 people observed),

p=0.2 (probability that a person does not cover their mouth when sneezing).

So, the probability mass function for the given scenario is:

P(X=k)=(10/k) .
`0.2^(k)`.
`0.8^(10-k)`

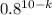
This formula will give you the probability of observing exactly k people out of the 10 not covering their mouth when sneezing.