The radius r that minimizes the construction materials necessary is approximately 3.02 centimeters.
To determine the radius of the cylinder that minimizes the construction materials necessary, we need to set up an optimization problem. The volume
V of a cylinder is given by the formula:
V=πr^2 h
where
r is the radius and ℎ is the height
In this case, we want to minimize the amount of construction materials used, which is related to the surface area
A of the cylinder. The surface area A of a cylinder is given by:
A=2πr^2 +2πrh
We are given that the volume V must be 178 cubic centimeters, so we can express h in terms of r using the volume formula:
h=
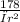
Now, substitute this expression for ℎ into the surface area formula:
A=2πr^2 +2πr
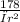
Simplify the expression:
A=2πr^2

To minimize A, take the derivative of A with respect to r and set it equal to zero:
 =4πr−
=4πr−

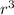 =
=
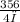
r =

Now, calculate
r≈ 3.02cm