Final Answer:
The correct solution set for the equation |s - 4| = 6 is option 3) s = -10 and s = 10.
Step-by-step explanation:
The given equation |s - 4| = 6 can be split into two cases:

For the first case, solving

For the second case, solving
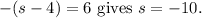
So, the solution set includes both
 making option 3) the correct answer. This is because the absolute value function yields two possible solutions for the given equation. It's essential to consider both the positive and negative cases when dealing with absolute value equations. In this context, the values
making option 3) the correct answer. This is because the absolute value function yields two possible solutions for the given equation. It's essential to consider both the positive and negative cases when dealing with absolute value equations. In this context, the values
 satisfy the original equation.
satisfy the original equation.
