Question

On October 9, 1992, a 12-kg meteorite struck a car in Peekskill, NY, creating a dent about 22 cm. The initial speed of the meteorite was 650 m/s. What was the average force exerted on the meteorite by the car?

Answer 1

To calculate the average force exerted on the meteorite by the car, we use the work-energy principle relating the change in the meteorite's kinetic energy to the work done by the force over the dislodged distance. The calculated average force is approximately 52,250,000 Newtons.

Step-by-step explanation:

The question involves calculating the average force exerted on a meteorite by a car during an impact. To find the average force, we'll use the formula derived from Newton's second law, which relates force, mass, and acceleration: F = ma.

However, since we don't have direct information about acceleration, we'll need to employ the work-energy principle, which states that the work done on an object is equal to the change in its kinetic energy. The work done by the car on the meteorite can be found using the formula W = Fd, where F is the force and d is the displacement; in this case, the depth of the dent is 22 cm or 0.22 m.

The kinetic energy change (ΔKE) is given by
`ΔKE = 0.5 * m * (vf^2 - vi^2)`, where m is the mass of the meteorite, vf is the final velocity (0 m/s, since the meteorite comes to rest), and vi is the initial velocity, which is 650 m/s. Since the initial kinetic energy
`(KE_initial = 0.5 * m * vi^2)` is converted to work done by the force to create the dent, we solve for the force using the formula F = ΔKE/d.

Performing the calculation:

`KE_initial = 0.5 * 12 kg * (650 m/s)^2`
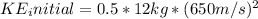
W = ΔKE = KE_initial
F = W/d = KE_initial/0.22 m

`F = (0.5 * 12 kg * 650 m/s * 650 m/s) / 0.22 m`
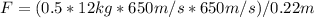
F = 11495000 N / 0.22 m
F ≈ 52250000 N

The average force exerted on the meteorite by the car is thus approximately 52,250,000 Newtons.