Question

Robert recorded the number of calls he made at work during the week:

Day Calls
Monday 20
Tuesday 12
Wednesday 10
Thursday 18

He expected to make 15 calls each day. To determine whether the number of calls follows a uniform distribution, a chi-square test for goodness of fit should be performed (alpha = 0.05).



Using the data above, what is the chi-square test statistic?
a.) 0.67

b.) 0.42

c.) 4.54

d.) 3.75

Answer 1

The chi-square test statistic c.) 4.54 . Therefore , c.) 4.54 is correct .

To perform a chi-square test for goodness of fit, we need to compare the observed frequencies (Robert's recorded calls) with the expected frequencies (15 calls each day).

The chi-square test statistic is calculated using the formula:

`X^(2)` = ∑
`((O_(i) -E_(i))^2)/(E_(i))`

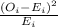
Where:

`O_(i)` is the observed frequency for each category (day),

`E_(i)` is the expected frequency for each category,

The summation is over all categories.

Let's calculate it step by step:

`X^(2)` =
`((20-15)^(2) )/(15)` +
`((12-15)^(2) )/(15)` +
`((10-15)^(2) )/(15)` +
`((18-15)^(2) )/(15)`

`X^(2)` =
`(25)/(15)` +
`(9)/(15)` +
`(25)/(15)` +
`(9)/(15)`

`X^(2)` =
`(68)/(15)`

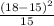
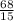
`X^(2)` ≈ 4.53

Now, comparing this value with the critical chi-square value at a significance level of 0.05 and degrees of freedom (number of categories - 1), we can determine whether to reject the null hypothesis.

For 3 degrees of freedom, the critical value is approximately 7.81.

Since 4.53<7.81, we do not reject the null hypothesis.