The goodness- of-fit needed to test the claim B. test statistic χ² = 0.523, critical value χ² = 9.488.Therefore , B. test statistic χ² = 0.523, critical value χ² = 9.488 is correct.
To test the claim that nonfatal occupational injuries and illnesses occur with equal frequency on different days of the week, you can use the chi-squared goodness-of-fit test.
The null hypothesis for this test is that the observed frequencies are equal to the expected frequencies for each category.
The alternative hypothesis is that the observed frequencies are not equal to the expected frequencies.
The test statistic (χ²) is calculated using the formula:
χ² = ∑
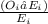
where
 is the observed frequency and
is the observed frequency and
 is the expected frequency for each category.
is the expected frequency for each category.
The expected frequency for each day of the week is the total number of injuries and illnesses divided by the number of days (5 in this case) because we are assuming equal frequencies for each day.
Expected frequency (
 ) for each day =
) for each day =
 =21.4
=21.4
Now, calculate the test statistic:
χ² =
 +
+
 +
+
 +
+
 +
+
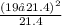
Calculating this, you get a test statistic
χ² ≈ 0.523.
Now, for a chi-squared goodness-of-fit test with 4 degrees of freedom (5 categories - 1), at a 0.05 significance level, the critical value is approximately 9.488 according to chi-squared distribution tables.